Возможности DSP обработки сигналов ядром Cortex M0 в контроллерах STM32F030
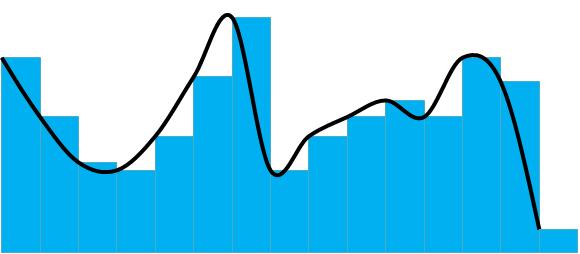
Низкая дискретизация звукового сигнала воспринимается человеческим ухом как посторонние шумы высоких частот – шипение в момент звукового воспроизведения. Природа этого звука показана ниже на рисунке. Чёрной линией показан реальный звуковой сигнал, а столбиками – его цифровое отображение. Резкие вертикальные фронты цифрового сигнала являются как раз источником шума высоких частот. Повышая дискретизацию сигнала во времени, вы автоматически снижаете уровень цифрового перепада и повышаете его частоту до «не воспринимаемой человеческим ухом».
Рис 1. Цифровой и аналоговый сигнал
Собственно говоря, повышением частоты дискретизации цифровых данных мы и займёмся. Для восстановления сигнала будем строить параболу 3-й степени по четырём точкам входных данных. Линейная алгебра начальных курсов ВУЗа утверждает, что по четырём точкам всегда можно найти одну параболу 3-й степени. Уравнение будет иметь вид:
Y (x) = D x³ + C x² + B x + A
Решение задачи состоит в поиске коэффициентов A, B, C и D. Имея данные по 4-м точкам грубого дискрета, мы получим систему 4-х уравнений с 4-мя неизвестными. Собственно говоря, наш микроконтроллер STM32F030F4P6 за 10 евроцентов (на объёмах 100000 штук в год) должен будет решать эту систему уравнений с частотой около 3 кГц. С частотой 3кГц происходит сэмплирование данных цифрового микрофона MP45 в проекте автора.
Имея математическое выражение функции мы всегда сможем передать её на выход с нужным нам временным и уровневым дискретом. Итак, для преобразования нам требуются данные по ближайшим 4-м точкам, подлежащим цифровому преобразованию. При этом мы будем восстанавливать только первую четверть сигнала.
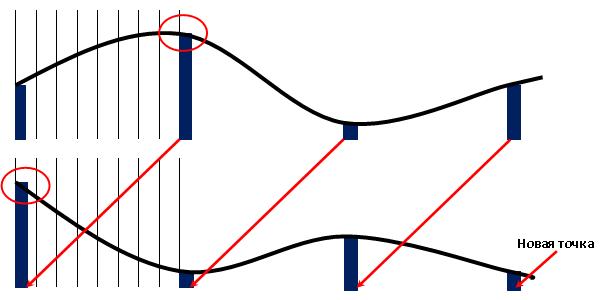
Рис 2. Алгоритм увеличения дискретизации
Как только появляются новые данные цифрового микрофона, происходит очередное вычисление коэффициентов параболы. При этом, для поиска новой параболы используются 3 старых точки, которые использовались в предыдущих вычислениях и одна новая. Точки, по которым происходит восстановление сигнала проходят очередь FIFO. Код выглядит очень просто:
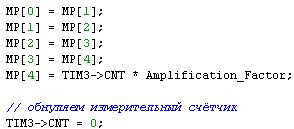
Рис 3. Код FIFO в проекте
Массив MP[] – это как раз точки, по которым будет производиться восстановление. Таймер 3 в проекте измеряет число импульсов цифрового микрофона. До цифрового преобразования производим усиление сигнала простым умножением его величины, после чего обнуляем счётчик.
Далее выполняется вычисление коэффициентов A, B, C, D по 4-м точкам:
Рис 4. Поиск коэффициентов A, B, C, D в проекте
Далее, по полученному уравнению происходит вычисление сразу 8-ми точек с высоким разрешением:
Рис 5. Восстановление функции. Код проекта
Выходные данные процесса складываются в выходной буфер Sound_Buffer[]. Чтобы ядро гарантированно успевало произвести цифровую обработку, выходной буфер звуковых данных имеет двойную структуру: из одной части происходит воспроизведение информации, а в другой – вычисление последующих звуковых данных. Данные буфера попадают в регистр ШИМ одного из таймеров через DMA, т.е. аппаратно.
На рисунке 2 красными кругами выделен излом восстанавливающей кривой, который возникнет после нового вычисления. Этот излом даст характерный спектр шумов. Чем будет выше порядок полинома = больше точек, по которым будет восстановлен сигнал, тем меньше будет величина излома (излом виднее всего будет при вычислении переходных точек по прямой линии вида y(x) = Bx+A). Правда, при этом, вырастет количество вычислений. Более того, в процессе вычисления случается переполнение 32-битных чисел, поэтому возникает потребность в операциях с плавающей запятой. В текущем проекте без оптимизации нагрузка ядра составляет примерно 70% времени. Время работы измерялось встроенным в ядро таймером SysTick. В силу того, что качество выходного звука существенно стало выше, автор принял решение использовать полином 4-й степени.
Стоит отметить, что математические вычисления можно оптимизировать. Например, операция деления может замениться на сдвиговую с некоторыми оговорками. В вычислениях есть несколько операций производящих деление на число степени 2. Ядро Cortex M0 не имеет аппаратной функции деления, поэтому такая оптимизация даст существенный эффект.
По времени контроллер успевает решать 5-ти мерную систему уравнений, однако автор не исключает переполнения 32-битных чисел в некоторых ситуациях, тут требуется детальное изучение предельных возможностей располагаемого диапазона чисел. Кроме того вычисление 5-мерной системы уравнений приблизит загрузку ядра к заветным 100%.
В целом автор пришёл к выводу, что контроллер STM32F030F4P6 за 10 евроцентов пригоден для решения некоторых DSP задач.
Компания IC-Contract желает вам успешных разработок.
Получить более подробную информацию по продукции STMicroelectronics вы можете, обратившись:
E-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Телефон: (343) 372-92-30
Задать вопрос техподдержке вы можете на нашем форуме.
